Le langage fonctionnel Caml

La construction d'un enregistrement de champs C ₁ , …, C_n est réalisée par le constructeur { C ₁ = ; …; C_n = }.

Par exemple :

#{Prénom = "Jean-" ^ "Paul"; Age = 5 + 1};;
- : enfant = {Prénom = "Jean-Paul"; Age = 6}

La sémantique du constructeur d'enregistrement est la suivante :

Deux enregistrements de même type sont structurellement égaux si les valeurs des champs de même nom sont structurellement égales.

L'accès à la valeur d'un champ est réalisée par l'opérateur « . ». Si v = { C ₁ = v ₁ ; … ; C_n = v _n } alors pour tout i de 1 à n , v . C_i = v_i . Par exemple :

#let jp = {Prénom = "Jean-Paul"; Age = 6};;
jp : enfant = {Prénom = "Jean-Paul"; Age = 6}
#jp.Age;;
- : int = 6

Si t est un type défini par t = { C ₁ : t ₁ ; … ; C _n : t _n } et si, pour tout i de 1 à n , v_i est une valeur de type t_i et F_i est un filtre de type t _i , alors :

{C1 = F1; …; Cn = Fn}

est un filtre de type t tel que :

env_filtré({C1 = v1; … ; Cn = vn}, {C1 = F1; … ;Cn = Fn}) = env_filtré(v1, F1)  …  env_filtré(vn, Fn)

Par exemple :

#let age = function {Prénom = _; Age = a} -> a;;
age : enfant -> int = <fun>
#age jp;;
- : int = 6

Puisqu'un nom de champ est attaché à un et un seul type, il est possible, dans un filtre, d'omettre les champs non concernés. La définition de age dans l'exemple précédent peut alors s'exprimer par :

#let age = function {Age = a} -> a;;
age : enfant -> int = <fun>

Une valeur d'un type union est construite par application de l'un des constructeurs de ce type. Par exemple :

#Carré (27. +. 0.5);;
- : forme = Carre 27.5
#Pile [3; 3 - 1; 3 - 2];;
- : pile = Pile [3; 2; 1]
#[Rouge; Jaune; Bleu];;
- : couleur_primitive list = [Rouge; Jaune; Bleu]

La sémantique d'un constructeur de valeur de type union est la suivante :

Deux valeurs d'un même type union sont structurellement égales si elles sont produites par l'application du même constructeur à deux valeurs structurellement égales.

Si t un type union défini par t = C₁ t₁ | … | C_n t_n et si F est un filtre de type t_i {t₁, …, t_n} alors :

Ci F

est un filtre de type t tel que env_filtré ( C _i F , C _i v ) = env_filtré ( F , v ).

Voici quelques exemples de manipulation de valeurs de type forme ou pile définis ci-dessus :

#let surface = function
    | Rectangle (lon, lar) -> lon *. lar
    | Carré côté -> côté *. côté
    | Cercle rayon -> 3.14 *. rayon *. rayon;;
surface : forme -> float = <fun>
#surface (Cercle 10.);;
- : float = 314
#let empiler i (Pile p) = Pile (i::p);;
empiler : int -> pile -> pile = <fun>
#let dépiler = function
    | Pile (i::p) -> i
    | Pile [] -> failwith "pile_vide";;
dépiler : pile -> int = <fun>
#dépiler (empiler 3 (Pile [1; 2]));;
- : int = 3

La fonction failwith appliquée à une chaîne de caractères m génère une exception, expliquée par le message m . Le traitement des exceptions est l'objet du chapitre suivant (chapitre IV).

Il est naturel que le corps d'une fonction s'appliquant à une valeur de type union comporte un cas pour chaque type de valeur composant ce type. Cette fonction ne pouvant être définie que par filtrage, si un cas n'est pas prévu, Caml le signalera (voir ci-dessus chapitre II, §III.C). Par exemple :

#let périmètre = function
    | Rectangle (lon, lar) -> 2. *. (lon +. lar)
    | Carré côté -> 4. *. côté;;
> Toplevel input:
>................function
> Rectangle (lon, lar) -> 2. *. (lon +. lar)
>    | Carré côté -> 4. *. côté..
> Warning: pattern matching is not exhaustive

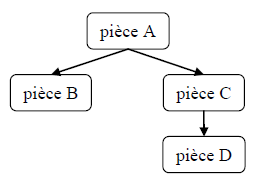
Figure 5.1 : Pièce composée

périmètre : forme -> float = <fun>

Le cas Cercle n'a pas été prévu. La fonction périmètre n'est donc applicable qu'aux rectangles et aux carrés :

#périmètre (Carré 4.);;
- : float = 16

mais pas aux cercles :

#périmètre (Cercle 10.);;
Uncaught exception: Match_failure ("", 1151, 1235)

(l'exception Match_failure … a été déclenchée par le système qui n'a pu filtrer la valeur Cercle 10.).

A titre d'exemple, nous allons programmer une calculette permettant d'évaluer des expressions arithmétiques construites à partir des nombres flottants et des cinq opérations classiques d'addition, de soustraction, de multiplication, de division et de calcul de l'opposé.

Il faut tout d'abord choisir une représentation des expressions soumises à la calculette. Nous les représenterons comme des valeurs du type récursif expr défini de la façon suivante :

#type expr =
    | Nb of float
    | Add of expr * expr
    | Soust of expr * expr
    | Mult of expr * expr
    | Div of expr * expr
    | Opp of expr;;
Type expr defined.

Par exemple, l'expression arithmétique ƒ{(5,2 „e (35,0 + 19,3)) sera représentée par la valeur de type expr suivante :

Opp (Mult (Nb 5.2, Add (Nb 35.0, Nb 19.3)))

Programmons maintenant notre calculette. L'évaluation d'une expression arithmétique représentée par une valeur de type expr sera réalisée par application à cette expression de la fonction eval définie de la façon suivante :

#let rec eval = function
    | Nb n -> n
    | Add (e1, e2) -> (eval e1) +. (eval e2)
    | Soust (e1, e2) -> (eval e1) -. (eval e2)
    | Mult (e1, e2) -> (eval e1) *. (eval e2)
    | Div (e1, e2) -> (eval e1) /. (eval e2)
    | Opp n -> -. (eval n);;
eval : expr -> float = <fun>

Remarquons encore une fois la souplesse apportée par la programmation par filtrage. Il suffit de prévoir un cas pour chaque constructeur du type expr.

Essayons :

#let mon_expression = Opp (Mult ((Nb 5.2), (Add (Nb 35.0, Nb 19.3))));;
mon_expression : expr = Opp (Mult (Nb 5.2, Add (Nb 35.0, Nb 19.3)))

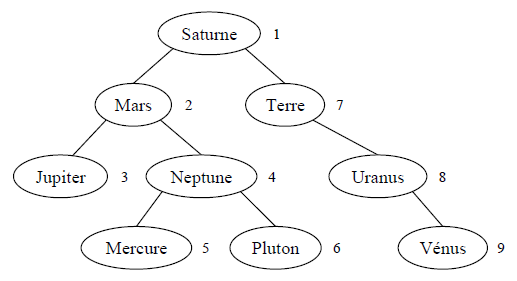
Figure 5.2: Un arbre binaire de recherche

#eval mon_expression;;
- : float = -282.36

Afin d'illustrer l'utilisation des types paramétrés, nous allons travailler sur une structure de données très classique : celle des arbres binaires de recherche.

Un arbre binaire est un ensemble fini de nœuds qui peut être soit un ensemble vide, soit un ensemble d'au moins un nœud tel que :

• un des nœuds constitue la racine de l'arbre ;
• l'ensemble des nœuds restants (excluant la racine) est partitionné en deux sous-ensembles dont chacun est un arbre binaire et qui sont appelés sous-arbre gauche et sous-arbre droit de la racine.

Chaque nœud contient une information appelée étiquette de ce nœud.

La figure 5.2 présente un exemple d'arbre binaire constitué de 9 nœuds numérotés de 1 à 9 et d'étiquettes respectives : « Saturne », « Mars », « Jupiter », « Neptune », « Mercure », « Pluton », « Terre », « Uranus » et « Vénus », qui sont les noms des neuf planètes du soleil. L'arbre binaire {1, 2, 3, 4, 5, 6, 7, 8, 9} a pour racine le nœud 1 dont le sous-arbre gauche est {2, 3, 4, 5, 6} et le sous-arbre droit est {7, 8, 9}. L'arbre binaire {2, 3, 4, 5, 6} a pour racine le nœud 2 dont le sous-arbre gauche est {3} et le sous-arbre droit {4, 5, 6}. L'arbre binaire {4, 5, 6} a pour racine le nœud 4 dont le sous-arbre gauche est {5} et le sous-arbre droit est {6}. L'arbre binaire {7, 8, 9} a pour racine le nœud 7 dont le sous-arbre gauche est vide et le sous-arbre droit est l'arbre binaire {8, 9}. L'arbre binaire {8, 9} a pour racine le nœud 8 dont le sous-arbre gauche est vide et le sous-arbre droit est l'arbre {9}. Les arbres binaires {3}, {5}, {6} et {9} ont pour racines respectives les nœuds 3, 5, 6 et 9 dont les sous-arbres gauche et droit sont vides.

Une catégorie intéressante d'arbres binaires est celle des arbres binaires de recherche, car ils offrent une représentation des ensembles permettant de tester l'appartenance d'un élément à un ensemble plus rapidement qu'en parcourant séquentiellement les éléments de cet ensemble.

Un arbre binaire de recherche est un arbre binaire dont les étiquettes sont les éléments d'un ensemble muni d'une relation d'ordre total et qui est tel que pour chaque nœud d'étiquette e , les étiquettes des nœuds de son sous-arbre gauche sont toutes inférieures à e et celles des nœuds de son sous-arbre droit sont toutes supérieures à e . L'arbre binaire de la figure 5.2, par exemple, est un arbre binaire de recherche.

Pour chercher si un élément x appartient à l'ensemble E des étiquettes d'un arbre binaire de recherche R , il suffit d'appliquer l'algorithme suivant : « si R est vide alors x n'appartient pas à E , sinon, si x est égal à l'étiquette de r alors x appartient à E , sinon, si x est inférieur à l'étiquette de r alors x appartient à E s'il appartient à l'ensemble des étiquettes du sous-arbre gauche de r , sinon, si x est supérieur à l'étiquette de r alors x appartient à E s'il appartient à l'ensemble des étiquettes du sous-arbre droit de R  » .

Testons, par exemple, si « Neptune » appartient à l'ensemble Noms_planètes des étiquettes de l'arbre binaire de recherche de la figure 5.2. On se place sur le nœud 1 racine de cet arbre : « Neptune » est inférieur à l'étiquette « Saturne » du nœud 1. On descend donc sur le nœud 2 racine du sous-arbre gauche du nœud 1 : « Neptune » est supérieur à l'étiquette « Mars » du nœud 2. On descend donc sur le nœud 4 racine du sous-arbre droit du nœud 2 : « Neptune » est égal à l'étiquette du nœud 2, il appartient donc à l'ensemble Noms_planètes .

Testons maintenant si « Io » appartient à l'ensemble Noms_planètes . On se place sur le nœud 1 : « Io » est inférieur à l'étiquette « Saturne » du nœud 1. On descend donc sur le nœud 2 : « Io » est inférieur à l'étiquette « Mars » du nœud 2. On descend donc sur le nœud 3 : « Io » est inférieur à l'étiquette « Jupiter » du nœud 3. Mais le sous-arbre gauche du nœud 3 est vide : « Io » n'appartient donc pas à l'ensemble Noms_planètes .

Montrons maintenant comment représenter de tels arbres en Caml et comment les manipuler au travers de trois opérations : insertion d'un élément, test d'appartenance d'un élément à un ensemble et tri par ordre croissant des éléments de l'ensemble.

On définit tout d'abord le type 'a arbre dont les instances sont des arbres binaires de recherche dont les nœuds ont pour étiquette des valeurs de type 'a :

#type 'a arbre =
    | Noeud of 'a arbre * 'a * 'a arbre
    | Vide;;
Type arbre defined.

L'insertion d'un noeud dans un arbre binaire nécessite la connaissance de la relation d'ordre dont est muni l'ensemble des étiquettes de cet arbre. Nous représenterons cette relation par une fonction qui appliquée à deux étiquettes e ₁ et e ₂ retourne Egal si e ₁ est égal à e ₂ , Inf, si e 1 est inférieur à e ₂ et Sup si e ₁ est supérieur à e ₂ . Les valeurs Inf, Egal et Sup sont les instances du type position défini par :

type position = Inf | Egal | Sup;;
#Type position defined.

L'insertion d'un nœud d'étiquette e dans un arbre binaire de recherche B produit un nouvel arbre binaire de recherche obtenu de la façon suivante :

• si B est vide, on produit un arbre binaire de recherche dont la racine a l'étiquette e et un sous-arbre gauche et un sous-arbre droit vide ;
• sinon, soit r l'étiquette de la racine de B , G le sous-arbre gauche de la racine de B et D son sous-arbre droit :
• si e est égal à r , alors l'arbre produit est B puisque l'ensemble de ses étiquettes contient déjà e,

• sinon, si e est inférieur à r alors l'arbre produit a une racine dont l'étiquette est r  ; le sous-arbre gauche de cette racine est le résultat de l'insertion du nœud d'étiquette e dans G et son sous-arbre droit est D,
• sinon, si e est supérieur à r alors l'arbre produit a une racine dont l'étiquette est r  ; le sous-arbre gauche de cette racine est G et son sous-arbre droit est le résultat de l'insertion du nœud d'étiquette e dans D .

D'où la définition de la fonction insérer_noeud qui retourne l'arbre binaire de recherche obtenu en insérant le nœud d'étiquette e dans l'arbre binaire de recherche arbre muni de la relation d'ordre comp :

#let rec insérer_noeud comp arbre e =
    match arbre with
        | Vide -> Noeud (Vide, e, Vide)
        | Noeud (g, r, d) ->
            (match (comp e r) with
                | Inf -> Noeud ((insérer_noeud comp g e), r, d)
                | Egal -> arbre
                | Sup -> Noeud (g, r, (insérer_noeud comp d e)));;
insérer_noeud : ('a -> 'a -> position) -> 'a arbre -> 'a -> 'a arbre = <fun>

En examinant le type de la fonction insérer on constate qu'il impose bien que le type 'a de l'étiquette du noeud à insérer soit le même que le type des étiquettes de l'arbre dans lequel cet élément est inséré et le même que le type des éléments auxquels est appliquée la fonction comp.

Testons maintenant cette fonction, en construisant un arbre binaire de recherche planètes dont les étiquettes sont les noms des neuf planètes du soleil. Cet arbre sera muni de la relation d'ordre alphabétique définie par la fonction comp_chaînes définie de la façon suivante :

let comp_chaînes n1 n2 =
    if n1 < n2 then
        Inf
    else
        if n1 = n2 then
            Egal
        else
            Sup;;
#comp_chaînes : 'a -> 'a -> position = <fun>

L'arbre de recherche planètes est construit en insérant itérativement dans un arbre binaire de recherche initialement vide les noeuds d'étiquettes : « Saturne », « Mars  » , « Neptune », « Jupiter », « Terre », « Uranus », « Mercure », « Pluton » et « Vénus ». Ce qui donne :

#let planètes =
    let rec insérer_liste_noeuds comp arbre le =
        match le with
            | [] -> arbre
            | e::le -> insérer_liste_noeuds comp
                (insérer_noeud comp arbre e)
                le
    in
        insérer_liste_noeuds comp_chaînes
            Vide
            ["Saturne"; "Mars"; "Neptune"; "Jupiter";
            "Terre"; "Uranus"; "Mercure"; "Pluton";
            "Vénus"];;
planètes : string arbre =
    Noeud
        (Noeud
            (Noeud (Vide, "Jupiter", Vide), "Mars",
            Noeud
                (Noeud (Vide, "Mercure", Vide), "Neptune",
                Noeud (Vide, "Pluton", Vide))),
            "Saturne",
            Noeud (Vide, "Terre", Noeud (Vide, "Uranus", Noeud (Vide, "Vénus", Vide))))

On vérifiera facilement que l'on obtient l'arbre binaire de recherche planètes est celui de la figure 5.2.

Pour rechercher si un élément e appartient à l'ensemble E des étiquettes d'un arbre binaire de recherche B , on applique la règle suivante, qui dérive directement de la règle de construction des arbres binaires de recherche :

• si B est vide, alors e n'appartient pas à E  ;
• sinon, soit r l'étiquette de la racine de B  :

• si e est égal à r alors e appartient à E,
• sinon, si e est inférieur à r alors rechercher e dans le sous-arbre gauche de la racine de B,
• • sinon, si e est supérieur à r alors rechercher e dans le sous-arbre droit de la racine de B .

D'où la définition de la fonction appartient qui retourne true si l'élément e appartient à l'arbre binaire de recherche arbre ou false sinon :

#let rec appartient comp arbre e =
    match arbre with
        | Vide -> false
        | Noeud (g, r, d) ->
            (match (comp e r) with
                | Inf -> appartient comp g e
                | Egal -> true
                | Sup -> appartient comp d e);;
appartient : ('a -> 'b -> position) -> 'b arbre -> 'a -> bool = <fun>

On peut tester cette fonction en recherchant « Neptune » puis « Io » dans l'ensemble des étiquettes de l'arbre binaire de recherche planètes :

#appartient comp_chaînes planètes "Neptune";;
- : bool = true
#appartient comp_chaînes planètes "Io";;
- : bool = false

On vérifie bien que « Neptune » appartient à cet ensemble et que « Io » n'y appartient pas.

Pour finir, nous allons définir une fonction trier, qui permet de construire la liste triée par ordre croissant des étiquettes de l'arbre binaire de recherche arbre. Pour réaliser ce tri, il suffit de parcourir récursivement cet arbre dans l'ordre sous-arbre gauche - racine - sous-arbre droit. La fonction trier peut donc être définie de la façon suivante :

#let rec trier arbre =
    match arbre with
        | Vide -> []
        | Noeud (g, r, d) ->
            (trier g) @ [r] @ (trier d);;
trier : 'a arbre -> 'a list = <fun>

Appliquons la fonction trier à l'arbre binaire de recherche planètes :

#trier planètes;;
- : string list =
["Jupiter"; "Mars"; "Mercure"; "Neptune"; "Pluton"; "Saturne"; "Terre";
"Uranus"; "Vénus"]

Cette application a bien pour valeur la séquence des neuf noms de planètes triée par ordre alphabétique.