II. Valeurs, environnements et expressions▲
Ce chapitre introduit les concepts de base du langage Caml : les valeurs manipulées ; les expressions, qui sont des calculs soumis à l'interprète Caml ; la définition de valeurs, qui consiste à leur donner un nom ; l' environnement qui mémorise les liaisons entre noms et valeurs et auquel Caml se réfère lors d'un calcul et enfin le fonctionnement de l'interprète lui-même.
II-A. Valeurs▲
Caml manipule des valeurs qui sont classées par types. Un type représente un ensemble de valeurs. Toute valeur appartient à un et un seul type. Il faut faire une distinction entre l'expression d'un type et son extension. L' expression d ' un type exprime la façon dont il est construit à partir d'autres types. L' extension d ' un type est l'ensemble des valeurs de ce type. Si t est une expression de type nous noterons ext ( t ) l'extension de t .
Les types constructibles en Caml seront étudiés pas à pas tout au long de ce cours. Pour débuter nous considérerons un sous-ensemble des types de Caml, que nous appellerons types de base . Ce sont les suivants :
- le type bool dont l'extension est constitué des valeurs true et false ( ext (bool) = {true, false}) ;
- le type int dont l'extension est l'ensemble des entiers appartenant à un intervalle dépendant de l'implémentation ([-2 30 , 2 30 -1] en général) ;
- le type float dont l'extension est l'ensemble des flottants appartenant à un intervalle dépendant de l'implémentation (si possible des flottants double précision à la norme IEEE) ;
- le type char dont l'extension est l'ensemble des caractères dont le code numérique est compris entre 0 et 255. Les caractères dont le code est compris entre 0 et 127 sont du standard ASCII et ceux dont le code est compris entre 128 et 255 dépendent de l'implémentation ;
- le type string dont l'extension est l'ensemble des chaînes de 0 à n caractères où n dépend de l'implémentation (65535 au minimum) ;
- le type unit dont l'extension ne contient qu'une seule valeur notée () et qui signifie « rien ».
II-B. Environnements▲
Une valeur peut être nommée. Un nom de valeur est :
- soit un identificateur différent des mots-clés réservés. Par exemple :
| Soit Env un environnement. VALEUR. Si v est une valeur de base de type t alors v est une expression telle que type(v, Env) = t et val(v, Env) = v. NOM DE VALEUR. Si n est un nom de Env lié à une valeur v de type t, alors n est une expression telle que type(n, Env) = t et val(n, Env) = v. EGALITE ET INEGALITE. Si e1 et e2 sont des expressions telles que type(e1, Env) = type(e2, Env) et op {=, <>} alors e1 op e2 est une expression telle que type(e1 op e2, Env) = bool et val(e1 op e2, Env) = val(e1, Env) op val(e2, Env). OPPOSE D'UN ENTIER. Si e est une expression telle que type(e, Env) = int alors -e est une expression telle que type(-e, Env) = int et val(-e, Env) = -val(e, Env). OPERATIONS ARITHMETIQUES SUR LES ENTIERS. Si e1 et e2 sont des expressions telles que type(e1, Env) = int et type(e2, Env) = int et op {+, -, *, /, mod} alors e1 op e2 est une expression telle que type(e1 op e2, Env) = int et val(e1 op e2, Env) = val(e1, Env) op val(e2, Env). COMPARAISONS D'ENTIERS. Si e1 et e2 sont des expressions telles que type(e1, Env) = int et type(e2, Env) = int et si op {<, <=, >=, >} alors e1 op e2 est une expression telle que type(e1 op e2, Env) = bool et val(e1 op e2, Env) = val(e1, Env) op val(e2, Env). OPERATIONS SUR LES FLOTTANTS. Les opérateurs -. +. -. *. /. <. <=. >=. >. sont définis sur les flottants de façon analogue aux opérateurs - + - * / < <= >= > sur les entiers. CONCATENATION DE CHAINES (^). Si e1 et e2 sont des expressions telles que type(e1, Env) = string et type(e2, Env) = string alors e1 ^ e2 est une expression telle que type(e1 ^ e2, Env) = string et val(e1 ^ e2, Env) = val(e1, Env) concaténé avec val(e2, Env). EXPRESSION PARENTHESEE. Si e est une expression alors (e) une expression telle que type((e), Env) = type(e, Env) et val((e), Env) = val(e, Env). |
Figure 1.1 : Les expressions de base
lon lar prénom1- soit un symbole d'opérateur précédé du mot-clé prefix. Par exemple :
prefix + prefix >=Les noms de valeurs sont aussi appelés variables . Ils doivent être différent des mots-clés réservés de Caml comme cela est classique dans la plupart des langages de programmation.
Une liaison est une association entre un nom et une valeur. Une liaison entre un nom n et une valeur v de type t sera notée :
n : t = vPar exemple :
lon : int = 15Un environnement est un ensemble de liaisons. Par exemple :
{lon : int = 15, lar : int = 5}Au début d'une session Caml il existe un environnement initial qui contient des liaisons prédéfinies, nous l'appellerons Env _ init .
Un environnement peut être étendu par un autre environnement. L'extension d'un environnement Env 1 par un environnement Env 2 , que nous noterons Env 1 Env 2 , est obtenue en ajoutant les liaisons de Env 2 aux liaisons de Env 1 dont le nom n'est pas présent dans Env 2 . On a :
Env1  Env2 = {n : t = v | n  Env1 et n  Env2 }  Env2On constate que cette opération à pour effet de ne garder que les liaisons les plus récentes de chaque nom. Par exemple :
{lon : int = 10}  {lon : int = 15, lar : int = 5} = {lon : int = 15, lar : int = 5}II-C. Expressions▲
Une expression est une construction Caml destinée à être évaluée. Toute expression a un type et une valeur. Le type d'une expression est déterminé (on dit aussi synthétisé) par Caml avant son évaluation.
Le type et la valeur d'une expression Caml dépendent de l'environnement dans lequel elle est évaluée. Si e est une expression et Env un environnement nous noterons :
type(e, Env)et :
val(e, Env)le type et la valeur de e dans Env . Par la suite nous dirons qu'une expression e est valide dans un environnement Env , si type ( e , Env ) est calculable.
Les types et les expressions valides en Caml seront étudiés pas à pas tout au long de ce cours. Pour débuter nous considérerons un sous-ensemble d'expressions (voir Figure 1.1), que nous appellerons de base, qui sont construites à partir des valeurs, des noms de valeur, et d'opérateurs sur les entiers, les flottants et les chaînes de caractères.
Considérons, par exemple, l'environnement :
Env = {lon : int = 15, lar : int = 5}On a :
type(2, Env) = int
type(lon, Env) = int
type(lar, Env) = int
type(lon + lar, Env) = int
type(2 * (lon + lar), Env) = intet :
val(2 * (lon + lar), Env)
= val(2, Env) * val((lon + lar), Env)
= 2 * val(lon + lar, Env)
= 2 * (val(lon, Env) + val(lar, Env))
= 2 * (15 + 5)
= 40II-D. Alternative▲
Il est souvent nécessaire d'effectuer des calculs qui dépendent d'une condition. Pour cela Caml dispose d'une construction particulière : l' alternative . Une expression alternative a la forme suivante :
if e1 then e2 else e3où e 1 est une expression de type bool et e 2 et e 3 sont des expressions de même type. Par exemple :
#if 10 > 5 then "Evidemment !" else "Bizarre !";;
- : string = "Evidemment !"Les règles de typage et d'évaluation d'une alternative sont les suivantes :
|
TYPE ET VALEUR D'UNE ALTERNATIVE. Si
Env
est un environnement et
e
1
,
e
2
,
e
3
sont des expressions telles que
type
(
e
1
,
Env
) = bool et
type
(
e
2
,
Env
) =
type
(e
3
,
Env
) =
t
alors :
type (if e 1 then e 2 else e 3 ) = t , val (if e 1 then e 2 else e 3 , Env ) = si val ( e 1 , Env ) = true alors val ( e 2 , Env ) sinon val ( e 3 , Env ). |
On constate que selon la valeur de la condition, soit e 2 , soit e 3 sont évaluées mais pas les deux.
Il est possible d'omettre la partie else. On a :
if e1 then e2  if e1 then e2 else ()ce qui implique que l'expression e 2 soit elle-même de type unit.
Les expressions suivantes sont équivalentes à l'alternative :
e1 & e2  if e1 then e2 else false,
e1 or e2  if e1 then true else e2Par exemple :
#(true or false) & true;;
- : bool = trueII-E. Définitions▲
II-E-1. Définitions globales▲
Une définition globale nomme des valeurs pour la durée d'une session. C'est une phrase qui a la forme suivante :
let n1 = e1 and … and nk = ek;;où n 1 , …, nk sont des noms de valeurs et e 1 , …, e k des expressions. Elle a pour effet, pour tout i de 1 à n , de donner le nom n i à la valeur de l'expression e i . Cette valeur constitue la définition de n i . Par exemple :
#let deux_fois_pi = 2. *. 3.14;;
deux_fois_pi : float = 6.28
#let lon = 15 and lar = 5;;
lon : int = 15
lar : int = 5La définition de deux_fois_pi est 6.28, celle de lon est 15 et celle de lar est 5.
Une définition globale a pour effet d'étendre l'environnement courant en cours par les liaisons introduites par la clause let. Soit Env_courant cet environnement, la définition let n1 = e1 and … and nk = ek le transforme en :
Env_courant  Env_def(let n1 = e1 and … and nk = ek, Env_courant).où Env_def calcule l'environnement ajouté par l'ensemble des liaisons introduites par une clause let selon la règle suivante :
|
ENVIRONNEMENT AJOUTE PAR UNE DEFINITION NON RECURSIVE. Si
Env
est un environnement et pour tout
i
de 1 à
k
,
n
i
est un nom de valeur et
e
i
est une expression telle que
type
(
e
i
,
Env
) =
t
i
, alors :
Env_def (let n 1 = e 1 and … and nk = e k , Env ) = { n 1 : t 1 = val ( e 1, Env ), …, nk : tk = val ( ek , Env )}. |
Par exemple, si l'environnement courant est :
Env_init  {rayon : float = 10., pi : float = 3.14}la définition :
let surface = 2. *. pi *. rayon;;le transforme en :
Env_init  {rayon : float = 10., pi : float = 3.14, surface : float = 62.8}La liaison établie par la définition globale d'un nom reste valable pendant toute la session. Pour la changer il faut redéfinir ce nom, ce qui générera une nouvelle liaison qui cachera l'ancienne. De plus cette redéfinition n'aura aucun effet sur les définitions antérieures ayant utilisé ce nom. Par exemple :
#let annee_courante = 1998;;
annee_courante : int = 1998
#2000 - annee_courante;;
- : int = 2
#let age = annee_courante - 1981;;
age : int = 17
#let annee_courante = 1999;;
annee_courante : int = 1999
#2000 - annee_courante;;
- : int = 1
#age;;
- : int = 17La valeur de age a été calculée avec l'ancienne valeur de l'année courante et n'a pas été affectée par la redéfinition de celle-ci.
Les noms définis dans une même clause let doivent être tous différents. Si ce n'est pas le cas Caml le signale. Par exemple :
#let lon = 5 and lon = 10;;
> Toplevel input:
>let lon = 5 and lon = 10;;
> ^^^
> Variable lon is bound twice in this pattern.Notons de plus, que les liaisons établies par une clause let ne sont visibles qu'une fois que cette clause a été évaluée. Dans l'exemple suivant :
#let cote = 10 and périmètre = 4 * cote;;
> Toplevel input:
>let cote = 10 and périmètre = 4 * cote;;
> ^^^^
> Variable cote is unbound.La liaison cote = 10 n'est pas visible dans la définition de périmètre. Pour qu'elle le soit il faut réaliser deux définitions successives :
#let cote = 10;;
cote : int = 10
#let périmètre = 4 * cote;;
périmètre : int = 40II-E-2. Définitions locales▲
La construction d'une expression peut être facilitée en nommant certaines sous-expressions dans des définitions locales à cette expression. Pour cela, Caml dispose d'un type particulier d'expression, que nous appellerons expression à définitions locales , qui a la forme suivante :
let n1 = e1 and … and nk = ek in eoù n 1 , …, nk sont des noms de valeurs, e 1 , …, ek sont des expressions et e est une expression. Par exemple :
#8 * (let lon = 15 and lar = 5 in 2 * (lon + lar));;
- : int = 320Les règles de typage et d'évaluation d'une expression à définitions locales sont les suivantes :
| TYPE ET VALEUR D'UNE EXPRESSION A DEFINITIONS LOCALES. Si Env est un environnement et pour tout i de 1 à k, ni est un nom de valeur, ei est une expression valide dans Env, et e est une expression telle que type(e, Env Env_def(let n1 = e1 and … and nk = ek, Env)) = t, alors : type(let n1 = e1 and … and nk = ek in e, Env) = t, val(let n1 = e1 and … and nk = ek in e, Env) = val(e, Env Env_def(let n1 = e1 and … and nk = ek, Env))}. |
On remarque que l'environnement est étendu par les définitions locales pour la durée de l'évaluation de l'expression e .
Concernant la duplication des noms et la visibilité des liaisons établies, les règles sont les mêmes que pour les définitions globales (§I.E.1). Notamment pour définir des noms locaux qui dépendent les uns des autres, il faut d'imbriquer les expressions à définitions locales. Par exemple :
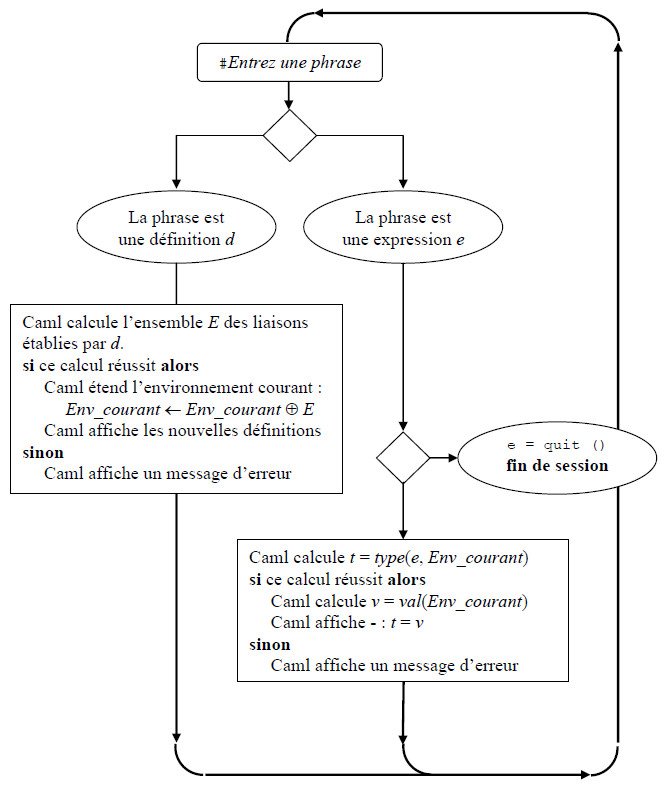
Figure 1.2 : La boucle de l ' interprète Caml
let lon = 15 and lar = 5 and hauteur = 30 in
let surface = lon * lar in surface * hauteur;;
- : int = 2250II-F. L'interprète Caml▲
La figure 1.2 schématise l'interaction entre le programmeur et l'interprète Caml au cours d'une session interactive.